angel
Matrix Factorization
Matrix Factorizaiton是推荐系统中常用的矩阵分解算法,将用户、商品抽象为K维向量,将用户-商品矩阵分解为用户矩阵和商品矩阵的乘积。
1. 算法介绍
MF的主要思想是把用户、商品的特征抽象为k维向量表示。
用户-商品评分矩阵(简称评分矩阵),是推荐系统中常用的数据表示方法,用一个矩阵表示用户对商品的打分。矩阵的每行代表一个用户,每列代表一个商品,每个元素代表对应用户对商品的评分,如图一所示。在大多数情况下商品数量巨大,每个用户只对极小部分商品有评分,所以评分矩阵一般非常稀疏,即评分矩阵中的绝大多数元素为0。MF算法把评分矩阵分解为用户-特征矩阵(简称用户矩阵)和特征-商品矩阵(简称商品矩阵)。
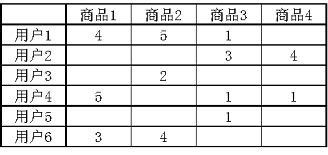
设数据集有M个用户,N个商品:评分矩阵用Y表示,Y的维度为:M×N,y_{ij} 表示第i个用户对第j个商品的评分;MF算法把评分矩阵Y分解为用户矩阵U和商品矩阵V的乘积,U的维度为M×k,每一行代表一个用户u_i,u_i是一个k维特征向量;V的维度为k×N,每一列代表一个商品v_j, v_j是一个k维特征向量;k是MF算法指定的值,代表特征向量的维度。我们以用户向量u_i和商品向量v_j的乘积作为用户i对商品j评分的预测值,记为y_{ij},如图二所示:
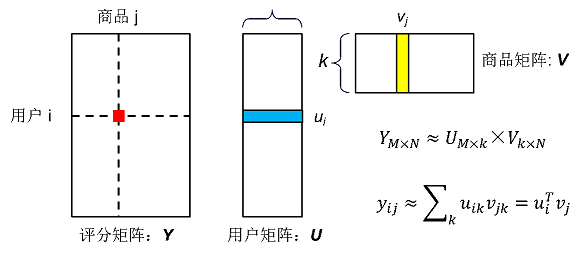
Gradient Descent Matrix Factorizaion
用户i对商品j的实际评分为y_{ij}预测值与真实值之差记为e_{ij},即:e_{ij}=y{ij}-u_i \cdot v_j。 MF算法的学习目标是最小化预测评分与真实评分之间的差距:
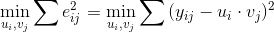
为了防止模型过拟合,加入L2正则项:
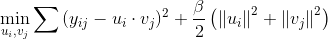
其中: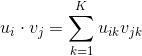
用梯度下降法最小化目标函数,得到用户特征向量u_i、商品特征向量v_j的更新公式为:
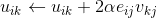
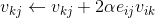
2. 分布式实现 on Angel
模型存储
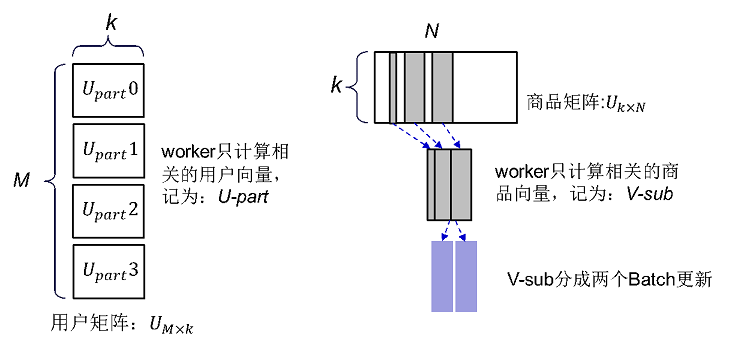
- 商品矩阵存放在PS,用户矩阵存放在Worker,PS和Worker间传输商品矩阵V即可,不需要传输用户矩阵U。
- 由用户向量的更新公式可知,用户向量的计算只和这个用户的评分数据有关,用户间相互独立,因此我们把用户矩阵U按照用户切分成多个子块存储在多个Worker,每个Worker只计算自己训练数据相关的用户的向量,记为:U-part,维度是:这个Worker分配到的用户数×k。
模型计算
Angel用梯度下降法学习MF模型,为了减少计算量和网络通信、提高计算效率,对算法做了以下设计:
-
因为商品向量的计算只和对它的评分相关,Worker上的训练数据可能只包含商品集合中的一部分商品的评分信息,这个Worker只能计算出这部分商品向量的梯度值,对无评分的商品计算的梯度值永远等于0,所以每次迭代只从PS拉取有评分的商品的向量即可,是整个商品矩阵的一个子集,记为V-sub矩阵。
-
当商品数量很大且k是一个比较大的值时,V-sub矩阵仍然可能超过了单个Worker的内存,而商品向量之间的更新相互独立,所以我们设计分批更新V-sub矩阵。每次迭代分成多个批计算,每批只从PS获取V-sub的一部分,用这部分商品向量更新Worker的用户矩阵,计算这部分商品向量的更新值推送给PS。
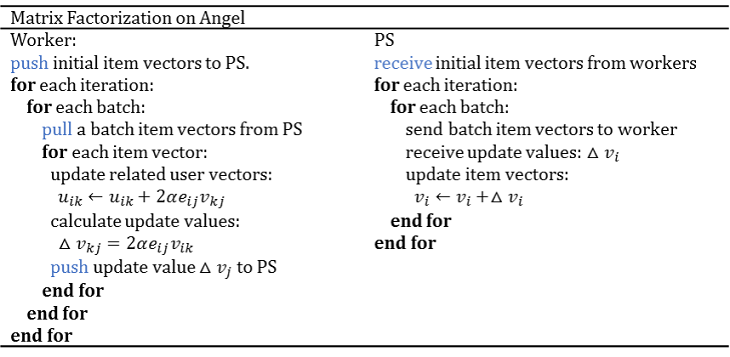
算法逻辑
Matrix Factorization on Angel的算法逻辑如下所示:
3. 运行 & 性能
输入格式
MF训练数据的格式:
用户ID,商品ID:评分,…,商品:评分
一个用户的所有评分存储在一行。
如下图所示:
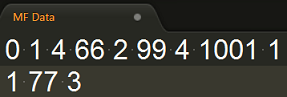
- ID为0的用户对ID为1、66、99、1001的商品评分分别为4、2、4、1
- ID为1的用户对ID为77的商品评分为3。
参数
- IO参数
- angel.train.data.path:输入数据路径
- angel.save.modelPath:商品特征矩阵保存路径
- angel.ml.mf.usermodel.output:用户特征矩阵保存路径
- angel.log.path:LOG保存路径
- 算法参数
- ml.mf.rank:用户、商品特征向量的维度
- ml.mf.item.num:商品数量
- ml.mf.lambda:正则化系数
- ml.mf.eta:学习速率
- ml.mf.row.batch.num:每次迭代的batch数
提交命令
./bin/angel-submit \ --angel.app.submit.class com.tencent.angel.ml.matrixfactorization.MatrixFactorizationRunner \ --action.type train \ --angel.train.data.path $input_path \ --angel.save.model.path $model_path \ --angel.ml.mf.usermodel.output $usermodelpath \ --angel.log.path $logpath \ --angel.worker.memory.mb 10000 \ --angel.ps.memory.mb 8000 \ --angel.worker.task.number 1 \ --angel.ps.number 2 \ --angel.workergroup.number 5 \ --ml.mf.item.num 17771 \ --ml.mf.row.batch.num 3 \ --ml.mf.rank 200 \ --ml.epoch.num 5 \ --ml.mf.lambda 0.01 \ --ml.mf.eta 0.00005 \